Para provar a seus contemporâneos que um monarca, por mais poderoso que seja, não é nada sem seus súditos, um brâmane hindu chamado Sessa inventou um dia o jogo de xadrez.
Quando este jogo foi apresentado ao rei das Índias, este ficou tão maravilhado com a sua engenhosidade e a grande variedade de suas combinções que mandou chamar o brâmane para recompensá-lo pessoalmente:
– Quero recompensar-te por tua extraordinária invenção – disse o rei. – Escolhe tu mesmo a recompensa e a receberás imediatamente. Sou suficientemente rico para realizar teu desejo mais absurdo.
O sacerdote pediu que o rei lhe desse um pouco de tempo para pensar em sua resposta. E, no dia seguinte, espantou a todos com a incrível modéstia do seu pedido.
– Meu bom soberano – exclamou ele –, queria que me désseis a quantidade de trigo necessária para encher as 64 casas do meu tabuleiro. Um grão para a primeira, dois para a segunda, quatro para a terceira, oito para a quarta, dezesseis para a quinta, e assim por diante. Em resumo, queria que fosse colocado em cada caso o dobro de grãos que na casa precedente.
– Não acredito que sejas tão tolo a ponto de fazer um pedido tão modesto! – exclamou o rei, surpreso. – Poderias ofender-me com um pedido tão indigno de minha benevolência e tão desprezível diante do que eu poderia oferecer-te. Mas que seja! Se é este o teu desejo, meus servidores te trarão teu saco de trigo antes do cair da noite.
O brâmane sorriu e deixou o palácio.
À tarde, o soberano se lembrou da promessa e se informou com seu ministro para saber se o louco Sessa tinha tomado posse de sua magra recompensa.
– Soberano – disse o alto dignitário –, vossas ordens estão sendo executadas. Os matemáticos de vossa augusta corte estão determinando o número de grãos que devem ser dados ao sacerdote.
O semblante do reu se obscureceu. Ele não estava habituado a uma execução tão morosa de suas ordens.
À noite, antes de se deitar, o rei insistiu uma vez mais para saber se o brâmane já recebera seu saco.
– Ó rei – disse o ministro, hesitante –, os matemáticos ainda não chegaram ao fim de suas operações. Estão trabalhando sem descanso e esperam terminar sua tarefa antes do amanhecer.
É preciso notar que os cálculos se revelaram muito mais longos do que se pensara. Mas o rei não quis saber de nada, e ordenou que o problema fosse resolvido antes do seu despertar.
Mas no dia seguinte esta ordem ainda ficou sem efeito, o que incitou o monarca enfurecido a despedir os calculadores.
Nesse momento, um dos conselheiros do monarca interveio:
– Ó soberano, tendes razão de despedir estes calculadores incompetentes. Eles utilizavam métodos mouito antigos. Ainda estavam usando as possibilidades numéricas de seues dedos e as colunas sucessivas de uma tábua de contar. Disseram-me que os calculadores da província do noroeste do reino empregam já há algum tempo um método bem superior e mais rápido do o deles. Parece que é mais rápido e mais fácil de guardar. Operações que exigiriam de seus matemáticos vários dias de trabalho difícil representariam, para estes de quem vos falo, um trabalho de algumas horas!
Seguindo esses conselhos, foi chamado um desses engenhosos matemáticos, que, após ter resolvido o problema em tempo recorde, se apresentou ao rei para comunicar o resultado.
– A quantidade de trigo pedida – disse num tom grave – é imensa.
Mas o rei retorquiu que, por maior que ela fosse, seus celeiros não seriam esvaziados.
Estupefato, ouviu então do sábio as seguintes palavras:
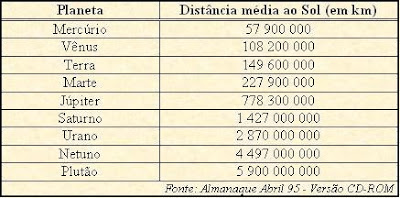
– Ó soberano, apesar de toda vossa potência e riqueza, não está em vosso poder oferecer uma tal quantidade de trigo. Ela está muito além do conhecimento e do uso de que dispomos dos números. Saibais que, mesmo se esvaziásseis todos os celeiros de vosso reino, o resultado obtido seria desprezível em comparação com esta enorme quantidade. Aliás, ela não pode ser encontrada nem no conjunto de todos os celeiros da Terra. Se desejais de fato oferecer esta recompensa, será preciso começar secando os rios, os lagos, os mares e os oceanos, depois derreter toda neve e as geleiras que recobrem as montanhas e certas regiões do mundo e transformar, enfim, tudo em campos de trigo. E só depois de ter semeado setenta e três vezes seguidas o total desta superfície podereis saldar esta pesada dívida. Mas, para uma quantidade desta ordem, seria preciso armazenar um volume de trigo de quase doze bilhões e três milhões de metros cúbicos e construir um celeiro de cinco metros de largura, dez de comprimento e ... treze milhões de quilômetros de profundidade (ou seja, uma altura igual a duas vezes a distância da Terra ao Sol)!
– Na verdade – acrescentou o sábio –, os grãos de trigo que este brâmane vos pediu são exatamente em número de
18.446.744.073.709.551.615
Depois, o calculador explicou ao soberano as características da numeração revolucionária dos sábios de sua região natal, ensinando-lhe em seguida os métodos de cálculo correspondentes, além de lhe fornecer nos seguintes termos a justificação de seus próprios cálculos:
– De acordo com o pedido do bramâne, seria preciso colocar:
1 grão de trigo na primeira casa;
2 grãos de trigo na segunda;
4 grãos (ou seja, 2 x 2) na terceira;
8 grãos (ou seja, 2 x 2 x 2) na quarta;
16 grãos (ou seja, 2 x 2 x 2 x 2) na quinta;
e assim por diante, multiplicando sempre por 2 de uma casa para a outra. Assim, na 64ª casa seria preciso colocar tantos grãos quantas unidades há no resultado de 63 multiplicações sucessivas por 2 (isto é, 263 grãos). A quantidade pedida é, conseqüentemente, igual à soma desses 64 números (ou seja: 1 + 2 + 22 + ... + 263 ).
– Se acrescentásseis um grão a este número – prosseguiu o calculador –, haveria 2 grãos na primeira, logo 2 vezes 2 grãos nas duas primeiras. Na terceira, haveria então (2 x 2 + 2 x 2) grãos de trigo, isto é, 2 vezes 2 vezes 2 ao todo. Na quarta, o total seria (2 x 2 x 2 + 2 x 2 x 2), isto é, 2 vezes 2 vezes 2 vezes 2 grãos. Procedendo deste modo, de um em um chegaríeis a um total igual ao resultado de 64 multiplicações sucessivas por 2 (ou seja, 264). Ora, este número é igual ao produto de 6 vezes o produto de 10 multiplicações sucessivas por 2, sendo ele mesmo multiplicado pelo número 16.

– E – concluiu ele –, como este número foi obtido acrescentando uma unidade à quantidade procurada, o total de grãos é então igual a ele próprio menos um grão. Se efetuardes as operações precedentes segundo o método que vos ensinei, podereis ficar certo, ó soberano, de que a quantidade de grãos pedida é exatamente de dezoito quintilhões, quatrocentos e quarenta e seis quatrilhões, setecentos e e quarenta e quatro trilhões, setenta e três bilhões, setecentos e nove milhões, quinhentos e cinqüenta e um mil, seiscentos e quinze!
– Decididamente – respondeu o rei, muito impressionado –, o jogo que este brâmane inventou é tão engenhoso quanto é sutil o seu pedido! Quanto a teus métodos de cálculo, sua simplicidade iguala a sua eficácia. Diga-me agora, sábio homem, o que é preciso fazer para pagar uma dívida tão incômoda?
O outro refletiu um instante e disse:
– Fazer este brâmane esperto cair na sua própria armadilha. Proponha-lhe vir contar pessoalmente, grão por grão, toda a quantidade de trigo que ele teve a audácia de pedir. Mesmo se ele trabalhasse sem descanso dia e noite, à razão de um grão por segundo, só recolheria um metro cúbico em seis meses, uns vinte metros cúbicos em dez anos e ... uma parte inteiramente insignificante pelo resto de sua vida! ...
Georges Ifrah, Os números - a história de uma grande invenção - Editora Globo, 1996.




![clip_image001[19]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjkdkqcQDGMJoIE11FQPO38X73h6bVaRkc3PZSWOy0obqUl842Dd8qpwKyYJal_OSqEyolR-4pR7LtMBIQIMVLwrn1UEbhjiT6P9XyP0R3uyPn6i4gdwizY8njTwMlDU5p6ZLyJgHTT52o/)
![clip_image001[21]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgKL49_2tIFpcxE5RLEXygpgvasns7J_10pnIwS2EkBj7oydH7GdJbaaaZyNvkbC9ehJJMJlpnuoCGj5j-tIUrsUHczABX1eUg8p-5fQCNJRKx2wcshZ-xau7FZn5M1CM9yYyggVkFlpbU/)

![clip_image001[6]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjDjP8zM_95QyQhTLAS_NAEG5MwEoXcw9pev8sMjCXIUVJMNg1sh5Zrxt-wvtNLidP8E7gihI1mRlxQKa_l7OmWQQMgO6Lmkqc7EXQm1yf-_1V8TOzVGe504-HOLx4tW2tK7kdkG-dhK0o/)














![clip_image002[5]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhjUKcD7rsrqSUm1lLSSN2g0ILv0M57DbocQC_6ldeoHALz0Nh-iuan32qcldkJiz6pcOuFPWhAaT4kWfxvZ32EmzTDwrXs68atMuQfgh-QJjClIbf212-rEPFTwPz0p6ZtKWJKJejni6g/)
![clip_image002[7]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg2RfkkoG7Jgj1-_LBVMYubYJHpRlYO_NUT-qlYhRb-JOkB3AKoNzNHIWbW_GMTbGciK_5QDFKcdXID-qU9gCYCQZpfaGINoBWasgn8qPOq4yx_ccn5tSf8Ky2OLnjKO0uPcYoQ2qyJarE/)


![clip_image002[6]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjXJ3tP7DW9snT5f-0mSp_Depi7dzcY1ys4ltef6zc4Z9qrIBm-abjmwKaZpuo9GPWkxb_BqHrLDh0XVPcSsYu6HtUdv5kTAuBNLAhIPiFupvlbumBzfo7cB1OLT_1fv9jn4Qygr8Qfzs0/)