O conceito
 A construção e o desenvolvimento dos conjuntos numéricos aparece como resultado das necessidades que o ser humano teve, em algum período da história, de criar um símbolo que desse significado matemático a certas operações que até então não o tinham.
A construção e o desenvolvimento dos conjuntos numéricos aparece como resultado das necessidades que o ser humano teve, em algum período da história, de criar um símbolo que desse significado matemático a certas operações que até então não o tinham.
O conjunto dos números naturais
 É o primeiro conjunto de que se tem notícia. Foi criado a partir da simples necessidade que o homem tem de contar. É representado pelo símbolo N e formado pelos seguintes elementos:
É o primeiro conjunto de que se tem notícia. Foi criado a partir da simples necessidade que o homem tem de contar. É representado pelo símbolo N e formado pelos seguintes elementos:
N = {0, 1, 2, 3, 4, 5, ⋯}
O conjunto dos números inteiros
 É uma ampliação do conjunto dos números naturais. Nasceu da necessidade de se criar um símbolo que representasse, na operação de subtração, o resultado que se obtém quando de uma quantidade menor se pretende tirar uma maior. É representado pelo símbolo Z e formado pelos seguintes elementos:
É uma ampliação do conjunto dos números naturais. Nasceu da necessidade de se criar um símbolo que representasse, na operação de subtração, o resultado que se obtém quando de uma quantidade menor se pretende tirar uma maior. É representado pelo símbolo Z e formado pelos seguintes elementos:
Z = { ⋯, -3, -2, -1, 0, +1, +2, +3, ⋯}
O conjunto dos números racionais
 Os números racionais surgiram da necessidade de representar partes de um inteiro. É representado pelo símbolo Q e formado pelos seguintes elementos:
Os números racionais surgiram da necessidade de representar partes de um inteiro. É representado pelo símbolo Q e formado pelos seguintes elementos:

De maneira simplificada, os números racionais são aqueles que podem ser escritos na forma de fração, onde o numerador e o denominador são números inteiros.
O conjunto dos números irracionais
 Os números irracionais são aqueles que não podem ser escritos na forma de fração, sendo números decimais, infinitos e não-periódicos. É representado pelo símbolo I.
Os números irracionais são aqueles que não podem ser escritos na forma de fração, sendo números decimais, infinitos e não-periódicos. É representado pelo símbolo I.
Como exemplos de números irracionais podemos citar:




O conjunto dos números reais
 O conjunto dos números reais é uma expansão do conjunto dos números racionais que engloba não só os inteiros e os fracionários, positivos e negativos, mas também todos os números irracionais. É representado pelo símbolo R.
O conjunto dos números reais é uma expansão do conjunto dos números racionais que engloba não só os inteiros e os fracionários, positivos e negativos, mas também todos os números irracionais. É representado pelo símbolo R.

Resolvendo uma equação do 2º grau
Vamos encontrar as raízes da equação: x2- 6x + 10 = 0
Utilizando a fórmula de Bhaskara:
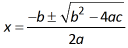



Não há como encontrar as raízes dessa equação pois não existe no conjunto dos números reais um número que elevado ao quadrado resulte em – 4 !!!!
O conjunto dos números complexos
O conjunto dos números complexos surgiu da necessidade de se encontrar as raízes não reais de equações de grau maior ou igual a 2 e dar um significado matemático às raízes quadradas de números negativos.
 Em 1545, Girolamo Cardano (1501-1576) falou das raízes quadradas de números negativos e, em 1572, Rafael Bombelli (1526-1572) percebeu que equações do tipo x2+a = 0 só poderiam ser resolvidas com o auxílio de números que mais tarde viriam a ser designados de imaginários por Descartes.
Em 1545, Girolamo Cardano (1501-1576) falou das raízes quadradas de números negativos e, em 1572, Rafael Bombelli (1526-1572) percebeu que equações do tipo x2+a = 0 só poderiam ser resolvidas com o auxílio de números que mais tarde viriam a ser designados de imaginários por Descartes.
 Foi criada, então, uma unidade imaginária a que Leonard Euler (1707-1783), em 1777, passou a representar pela letra i, de tal maneira que:
Foi criada, então, uma unidade imaginária a que Leonard Euler (1707-1783), em 1777, passou a representar pela letra i, de tal maneira que:

 Mas foi Caspar Wessel (1745-1818) que em 1797 utilizou pela primeira uma representação gráfica para os números complexos.
Mas foi Caspar Wessel (1745-1818) que em 1797 utilizou pela primeira uma representação gráfica para os números complexos.
 Entretanto, somente por volta de 1806, a partir de um trabalho publicado por Jean Robert Argand (1768-1822), a representação geométrica dos números complexos ganhou o devido respeito.
Entretanto, somente por volta de 1806, a partir de um trabalho publicado por Jean Robert Argand (1768-1822), a representação geométrica dos números complexos ganhou o devido respeito.
 Somente no século XVIII é que esses estudos foram formalizados pelo matemático Carl Friedrich Gauss (1777-1855) que, em 1832, utilizou pela primeira vez a expressão “número complexo”.
Somente no século XVIII é que esses estudos foram formalizados pelo matemático Carl Friedrich Gauss (1777-1855) que, em 1832, utilizou pela primeira vez a expressão “número complexo”.
Retomando a resolução da equação do 2º grau
Vamos encontrar as raízes da equação: x2- 6x + 10 = 0
Utilizando a fórmula de Bhaskara:







Chamadas de raízes complexas da equação.
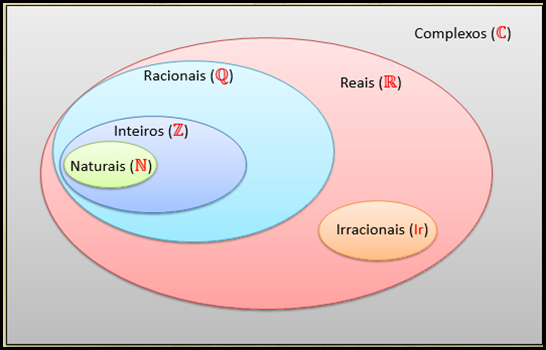
Os conjuntos numéricos
Francisco Ismael Reis

06/03/2019

















Nenhum comentário:
Postar um comentário