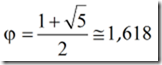Duas séries infinitas

Já tive a oportunidade, em momentos distintos, de escrever neste blog, sobre o número de ouro, representado pela letra grega φ (fi) e cujo valor é:

Pois bem motivado pela postagem anterior – Uma equação irracional – , vou escrever sobre duas expressões matemáticas que tem o formato de séries infinitas e cujo valor é surpreendente.

• A primeira delas é:

Vamos calcular seu valor:

Igualando essa expressão a x:

Elevando, agora, ambos os membros ao quadrado:

Observe que nesta última equação a expressão inicial, aquela que chamamos de x e que aparece assinalada em vermelho, se repete infinitamente, assim sendo, podemos escrever que:

 

Resolvendo essa equação do 2º grau com o auxílio da fórmula de Bhaskara:

Se considerarmos apenas a raiz positiva, temos que:

Que como vimos anteriormente, trata-se do número de ouro.

• A outra expressão é:

Também aqui, vamos chamar de x a essa expressão:

Repare que nesta última equação, a parte em vermelho é o próprio x, ou seja:

Multiplicando ambos os membros dessa equação por x, obtemos:

Que tem como raízes:

Considerando apenas a raiz positiva:

E mais uma vez, temos como solução o número de ouro.

Francisco Ismael Reis.

03/03/2019

Uma equação irracional

Raphael Sakamoto Ligero, um aluno meu do 3EM do Colégio Guilherme Dumont Villares bastante interessado pela Matemática, me propôs encontrar as soluções reais da seguinte equação irracional:

Apresento a seguir minha solução:
Observemos inicialmente que os valores de x encontram-se no intervalo real

valores esses que definem a condição de existência da equação.
Note que essa equação é equivalente a:

Que, por sua vez, é equivalente a:

Elevando ambos os membros ao quadrado, ficamos com:

Essa equação pode ser fatorada como apresentado a seguir:

De onde sai que:

 

     

As soluções x₁ e x₃, não satisfazem à condição de existência da equação, logo:

       e   

representam as soluções da equação.
A comprovação gráfica das soluções dessa equação é apresentada  no gráfico abaixo:

Francisco Ismael Reis

28/02/2019

Arredondamentos

Em muitas situações do dia a dia, principalmente quando trabalhamos com números muito grandes ou números com muitas casas decimais, não é necessário que o façamos com os valores exatos. Por vezes, para facilitar os cálculos e até mesmo a leitura desses números, é interessante que façamos arredondamentos.

Vamos considerar dois casos:

• Arredondamento com números decimais

Inicialmente devemos decidir com quantas casas decimais queremos trabalhar e eliminar aquelas que não nos interessam. Feito isso, vamos olhar para o primeiro algarismo à direita daqueles que permanecerão. Se esse algarismo for menor que 5, nada muda, caso contrário, aumentamos o último algarismo do número com que queremos ficar de 1 unidade.
Acompanhe os exemplos:

Número	Casas decimais	Arredondamento	Como fica
82,274369	4	82,2743|69	82,2744
82,274369	3	82,274|369	82,274
82,274369	2	82,27|4369	82,27
82,274369	1	82,2|74369	82,3

• Arredondamento com números inteiros

Com números grandes, o arredondamento é feito de acordo com a ordem desejada, seguindo-se a mesma lógica utilizada no arredondamento dos números decimais.
Relembremos como se classificam os números em classes e ordens.

Observe agora os exemplos a seguir:

Número	Ordem	Arredondamento	Como fica
419.735.237	dezena	419.735.23|7	419.735.240
419.735.237	centena	419.735.2|37	419.735.200
419.735.237	u. de milhar	419.735.|237	419.735.000
419.735.237	u. de milhão	419.|735.237	420.000.000

Francisco Ismael Reis.

04/01/2017.

O número do sapato

A história dos calçados começa quando o homem percebeu que seus pés eram sensíveis e precisavam de proteção para ajudá-lo a se locomover através dos diferentes tipos de solo, principalmente os mais pedregosos.
Acredita-se que o ofício de sapateiro tenha nascido com os antigos egípcios por volta de 1500 A.C.

Entretanto, foi no século XIII, na Inglaterra, que o rei Eduardo I estabeleceu que uma polegada (2,54 cm, o tamanho do seu polegar) seria o equivalente a 3 grãos de cevada secos e alinhados. Surgia, assim, a primeira padronização para se medir o tamanho dos sapatos e uma nova unidade métrica, o ponto. Dessa forma, ao pé de uma pessoa que medisse 40 grãos de cevada de comprimento, seria associado número 40. Esse padrão é utilizado, ainda hoje, na Inglaterra e nos Estados Unidos.
Países, como o Brasil, adotam sistemas diferentes desse, mas baseados na ideia de ponto. Aqui, o ponto equivale a 2/3 de cm (0,66 cm).
Para escrevermos a função que expressa o número do nosso sapato, vamos chamar de s à variável dependente que representa, em pontos, o número do sapato e de x à variável independente que representa, em centímetros, o comprimento do pé.
Assim:

Dessa maneira, a um pé cujo comprimento seja de 26 cm, corresponderá, em pontos, o número:

Francisco Ismael Reis

04/01/2017.

Uma curiosidade com números de 3 algarismos

Escolha um número qualquer de 3 algarismos e multiplique-o, sucessivamente, por 7, 11 e 13.
Observe os exemplos:
1) Escolhendo o número 217

217 x 7 = 1519
1519 x 11 = 16709
16709 x 13 = 217217

2) Escolhendo 539

539 x 7 = 3773
3773 x 11 = 41503
41503 x 13 = 539539

Experimente fazer o mesmo, escolhendo outros números.
Note que, qualquer que seja o número de três algarismos escolhido, o resultado final é formado pelo número escolhido, escrito duas vezes.
Tente achar uma explicação para isso.
31/12/2016

Palíndromos

 

 

Uma palavra, frase ou qualquer sequência de algarismos que tenha a propriedade de apresentar o mesmo resultado ao ser lida da direita para a esquerda ou da esquerda para a direita é chamada palíndromo.

O número 1234321 é palíndromo ou capícua.

Num palíndromo, são desconsiderados os sinais ortográficos, bem como os espaços entre palavras.

Abaixo, alguns exemplos de frases palíndromas.

 

1. A BASE DO TETO DESABA

2. A CARA RAJADA DA JARARACA

3. A DIVA EM ARGEL ALEGRA-ME A VIDA

4. A GRAMA É AMARGA

5. A MALA NADA NA LAMA

6. A TORRE DA DERROTA

7. ADIAS A DATA DA SAÍDA

8. AME O POEMA

9. AMOR A ROMA

10. ANOTARAM A DATA DA MARATONA

11. ANOTARAM A MARATONA

12. APÓS A SOPA

13. ARARA RARA

14. ATÉ O POETA

15. EVA ASSE ESSA AVE

16. LÁ VOU EU EM MEU OVAL

17. LIVRE DO PODER VIL

18. LUZ AZUL

19. O CASACO

20. O CASO DA DROGA DA GORDA DO SACO

21. O CÉU SUECO

22. O GALO AMA O LAGO

23. O LOBO AMA O BOLO

24. O ROMANO ACATA AMORES A DAMAS AMADAS E ROMA ATACA O NAMORO

25. ÓDIO DO DOIDO

26. ÓTO COME DOCE SECO DE MOCOTÓ

27. RIR, O BREVE VERBO RIR

28. ROMA ME TEM AMOR

29. SAIRAM O TIO SÁ E OITO MARIAS

30. SOCORRAM-ME SUBI NO ONIBUS EM MARROCOS

 

 

30/12/2016

Fazendo o dinheiro circular

Um viajante chega numa cidade e entra num pequeno hotel. Na recepção, entrega duas notas de R$ 100,00 e pede para ver um quarto.
Enquanto o viajante inspeciona os quartos, o gerente do hotel sai correndo com as duas notas de R$ 100,00 e vai até o açougue pagar suas dívidas com o açougueiro.
Este pega as duas notas e vai até um criador de suínos a quem, coincidentemente, também deve R$ 200,00 e quita a dívida.
O criador, por sua vez, pega também as duas notas e corre ao veterinário para liquidar uma dívida de R$ 200,00.
O veterinário, com as duas notas em mãos, vai até a farmácia quitar a sua dívida que coincidentemente era de R$ 200,00.
O dono da farmácia sai com o dinheiro em direção ao hotel, lugar onde, às vezes, se hospeda e que ultimamente não havia pago pelas acomodações. Valor total da dívida: R$ 200,00. Ele avisa ao gerente que está pagando a conta e coloca as notas em cima do balcão.
Nesse momento, o viajante retorna dos quartos e diz não ser o que esperava, pega as duas notas de volta, agradece e sai do hotel.
Ninguém ganhou ou gastou um centavo; porém, agora, toda a cidade vive sem dívidas, com o crédito restaurado e começa a ver o futuro com confiança!
MORAL DA HISTÓRIA: NÃO QUEIRA ENTENDER ECONOMIA!