Um repouso de dezoito séculos
| Embora estudadas pelo geômetra grego Apolônio de Pérgamo, que viveu no século III a.C., as cônicas só foram encontrar aplicação quando o alemão Kepler, em 1609, enunciou suas leis. Entre o seu estudo, por Apolônio, e a sua aplicação, por Kepler, as cônicas tiveramum repouso de dezoito séculos. Foi um longo e bem merecido repouso. |
As curvas definidas geometricamente e que só podem ser cortadas por uma reta qualquer de seu plano, em dois pontos reais ou imaginários, denominam-se curvas de segunda ordem ou do segundo grau.
Essas curvas – círculo, elipse, hipérbole e parábola (veja a foto acima) – são também denominadas cônicas, pois qualquer uma delas pode ser obtida por meio de uma seção plana feita no cone de revolução.
Vemos, na figura ao lado, um cone (de duas folhas) cortado de maneiras diferentes por um plano.
Se o plano cortar o cone no vértice vamos obter um ponto. Êsse ponto será o círculo degenerado ou uma elipse degenerada. Mas mesmo assim é, para o matemático, uma cônica. Sim, uma cônica degenerada.
Os planetas descrevem, em torno do Sol, elipses. O Sol ocupa precisamente um dos focos da elipse, que define a trajetória do planeta.
Há planetóides cujas órbitas têm excentricidade tão pequena que são consideradas como circulares. Já foi observado um cometa com órbita parabólica. Esse cometa (com órbita parabólica) passou uma vez nas vizinhanças do Sol e seguiu a sua jornada pelo infinito, para nunca mais voltar. Sim, caminha para o infinito, mas continua sua órbita, acompanhando o Sol.
Eis o que escreveu o poeta goiano Geraldo Vale, assegurando que os planetas jamais estudaram Geometria:
E estes mundos cegos, inconscientes, gravitando
em parábolas, em círculos, em elipses,
com perfeita harmonia e grandiosa beleza
e jamais estudaram Geometria?
Vemos, assim, que as cônicas são curvas tão notáveis e interessantes que despertam até a atenção dos poetas.
Do cilindro, por meio de uma transformação muito simples, podemos passar para o cone. E isso graças a um artifício bastante curioso.
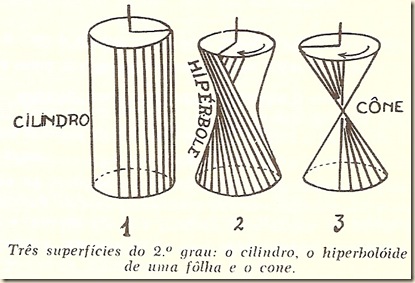
A figura abaixo nos mostra três superfícies do segundo grau com indicação de suas geratrizes retilíneas: o cilindro de base circular, o hiperbolóide de uma folha e o cone. Vemos que as duas folhas do cone são separadas por um ponto que é o vértice. É o caso em que o ponto separa as duas superfícies.
Sendo as geratrizes formadas por fios bem finos, podemos, por uma simples torção da base superior do cilindro, obter as outras superfícies, como indica a figura acima.
Estudadas por Apolônio, na Antigüidade, só foram as cônicas despertar a atenção dos homens com Kepler, quando este astrônomo alemão formulou as suas leis. Entre Apolônio e Kepler houve um intervalo de dezoito séculos.
Lidemos, pois, com as cônicas. Estudemos as suas propriedades. Vejamos quais são as suas aplicações. Elas precisam agir. Já tiveram um repouso de mil e oitocentos anos.
Malba Than, As maravilhas da Matemática, Editora Record, 1973.



Nenhum comentário:
Postar um comentário