Clique na imagem para ampliá-la.
Reflita sobre o que vê na ilustração, e deixe seu comentário.
A evolução
sábado, 27 de junho de 2009
Ano bissexto
Essa diferença de 6 horas corresponde a 1/4 de dia. Isso significa que a cada 4 anos existe uma diferença de 1 dia entre o ano-calendário e o ano solar.
A correção no calendário foi adotada pela primeira vez no Egito, em 238 AC. Com a introdução do calendário Juliano em 45 AC, adotou-se a regra de que todo ano divisível por quatro era bissexto. Porém, ainda assim, existia um erro de aproximadamente 1 dia a cada 128 anos.
No final do século XVI com a introdução do calendário Gregoriano, usado até hoje na maioria dos países, adotaram-se as seguintes regras para definir o ano bissexto:
| 1- Todo ano divisível por 4 é bissexto 2- Todo ano divisível por 100 não é ano bissexto 3- Mas se o ano for também divisível por 400 é ano bissexto |
Essas regras foram introduzidas para reduzir ainda mais o erro no calendário.
Para melhor entender:
- São bissextos todos os anos múltiplos de 400, p.ex: 1600, 2000, 2400, 2800
- Não são bissextos todos os múltiplos de 100 e não de 400, p.ex: 1700, 1800, 1900, 2100, 2200, 2300, 2500...
- São bissextos todos os múltiplos de 4 e não múltiplos de 100, p.ex: 1996, 2004, 2008, 2012, 2016...
- Não são bissextos todos os demais anos.
Ainda como curiosidade, a expressão bissexto vez ou outra é associada ao duplo seis (66) da expressão 366, o que expressa uma coerência mnemônica popular, porém, sem comprovação e o dia extra que serve como fator de correção não é o dia 29 de fevereiro, como a maioria das pessoas pensa, mas sim, o dia 24 do mesmo mês.
Francisco Ismael Reis.
27/06/2009.
sábado, 20 de junho de 2009
Fazer gol não é problema!
A imbatível equipe de futebol de salão do 1º ano A do Ensino Médio do Colégio Iavne de 2009, composta pelos atletas Allan M., Ernesto R., Johnny D., Johnny K., Marko D., Rafael H. e Samy K. que, devido à elevadissima qualidade técnica apresentada por seus jogadores, não tem a menor dificuldade em fazer gols no adversário, tem, entretanto, um pequeno problema:
| Como distribuir os sete atletas em campo, jogando 4 de cada vez e, de tal maneira que todos joguem o mesmo tempo, durante uma partida que tem a duração de 40 minutos? |
Preocupados em não perder a concentração para os jogos, ocupando-se com devaneios matemáticos, o que poderia acarretar uma ligeira diminuição na quantidade de gols que estão acostumados a “enfiar” nos adversários, a equipe me procurou, para que, na condição de professor de Matemática, os ajudasse a solucionar esse pequeno problema.
Para atender a tão simpático pedido, adotei, então, os seguintes procedimentos:
Procedimento 1
Como devem jogar quatro atletas simultâneamente, imaginei que cada um deles deveria ocupar, dentro de campo, uma das posições P1, P2, P3 e P4, cada uma das quais com tempo total de duração igual ao da partida, ou seja, 40 minutos.
Procedimento 2
Chamei cada um dos sete jogadores de J1, J2, J3, J4, J5, J6, e J7, respectivamente.
Procedimento 3
Distribuí todos os jogadores, imaginando cada um deles jogando durante um determinado “bloco unitário” de tempo, de mesma duração para cada um deles. A figura a seguir ilustra esse “bloco unitário”, correspondente a cada um dos atletas.
A quantidade de “blocos unitários” de tempo deve, portanto, ser um múltiplo de 7 (visto que são sete jogadores) e de 4 (visto que são quatro posições). Logo, o menor número de “blocos unitários” de que necessitamos é 7 x 4 = 28.
A figura a seguir ilustra uma das possíveis situações de distribuição, em campo, dos atletas através de seus “blocos unitários”.
Procedimento 5 - Conclusões
Observando a figura anterior podemos tirar as seguintes conclusões:
Cada posição é formada por 7 “blocos unitários” de tempo. Como cada posição tem o tempo de duração do jogo ou seja 40 minutos, cada “bloco unitário” de tempo equivale a 40/7 minutos, ou seja, aproximadamente 5 minutos e 42 segundos.
A solução apresentada não é única e talvez não seja a mais simples. Entretanto, a ideia de utilizar “blocos unitários” de tempo, possibilita aos jogadores e ao técnico uma forma simples de visualização dos atletas em campo e como consequência, facilidadede na escolha do melhor esquema tático.
Francisco Ismael Reis.
20/06/2009.
domingo, 14 de junho de 2009
Com 4 quatros!!!
Uma das características mais fascinantes da Matemática é o seu lado lúdico, através do qual, por meio do raciocínio lógico, ela nos instiga a vencer os desafios que nos são propostos.
Este interessante passatempo consiste em escrever os números inteiros de 0 a 9, através de uma expressão matemática na qual poderão ser utilizados apenas 4 quatros e os sinais operatórios de adição, subtração, multiplicação e divisão.
A figura ao lado nos mostra como isso pode ser conseguido. Procure, entretanto, antes de olhar para ela com mais atenção, obter alguns resultados.
Há quem diga ser possível escrever todos os números naturais de 0 a 100. Será que você, caro e paciente leitor, conseguirá, utilizando os mesmos recursos mais os símbolos operatórios de fatorial e raiz quadrada escrever mais alguns números?
Francisco Ismael Reis.
14/06/2009.
A origem dos nomes dos meses do ano
A palavra calendário deriva do latim calendarium ou livro de registro, que por sua vez derivou de calendae, que indicava o primeiro dia de um mês romano.
Alguns nomes dos meses do ano remontam à época do Império Romano.
Esse primeiro calendário romano tinha 10 meses, de 30 ou 31 dias, deixando fora dois meses de inverno.
A seguir a origem dos nomes dos meses do ano:
| Janeiro | Deriva do nome do deus Jano, o qual era representado com duas caras, uma olhando o ano que acaba e outra o que prinicipia. |
| Fevereiro | Mês do festival de Februália (purificação dos pecados), em Roma. |
| Março | Deriva do nome do deus Marte, deus da guerra e da justiça, da força e dos instintos básicos e masculino, por excelência. |
| Abril | Derivado do latim Aperire (por ser a época em que a terra se abre para produzir os seus frutos). Possível referência à primavera no Hemisfério Norte. |
| Maio | Acredita-se que se origine do nome de Maia, deusa do crescimento das plantas. |
| Junho | Mês que homenageia a deusa Juno, protetora das mulheres. |
| Julho | No primeiro calendário romano, que era de 10 meses, era chamado de quintilis (5º mês). Foi rebatizado posterirmente em homenagem ao imperador Júlio Cesar. |
| Agosto | Inicialmente nomeado de sextilis (6º mês), mudou em homenagem a César Augusto. |
| Setembro | Era o sétimo mês no primeiro calendário romano. Vem do latim septem. |
| Outubro | Na contagem dos romanos, era o oitavo mês. |
| Novembro | Vem do latim novem (nove). |
| Dezembro | Era o décimo mês do primeiro calendário romano. |
Francisco Ismael Reis.
14/06/2009.
domingo, 31 de maio de 2009
O problema das idades
O problema:
| Ao perguntar a idade do professor, um aluno recebeu do mesmo a seguinte “charada”: Juntos temos sete vezes a idade que você tinha quando eu tinha o dobro da idade que você tem. Daqui a dez anos eu terei o dobro da idade que você tiver. Se “P” é a idade do professor, e “A” a idade do aluno, determinar “P” e “A”. |
A solução:
Pela leitura do enunciado, podemos concluir a existência de três situações: uma presente, uma passada e uma futura.
Para melhor compreenssão dessas três situações, vamos utilizar o gráfico a seguir, representando a linha do tempo:
Na situação presente, a idade do professor será representada por P e a do aluno por A; Na situação passada, a idade do professor será representada por P – X e a do aluno por A – X; Na situação futura, a idade do professor será representada por P + 10 e a do aluno por A + 10.
Na situação presente o professor diz ao aluno:
Juntos temos sete vezes a idade que você tinha.
O que se traduz por: P + A = 7(A – X). Na situação passada, segundo o professor:
Quando eu tinha o dobro da idade que você tem.
O que se traduz por: P – X = 2A. Na situação futura:
Daqui a dez anos eu terei o dobro da idade que você tiver.
O que se traduz por: P + 10 = 2(A + 10).
Resolvendo, por qualquer processo, o sistema:
encontraremos que P = 50 e A = 20.
Francisco Ismael Reis
31/05/2009.
sábado, 30 de maio de 2009
O dodecaedro
 |
O número de faces de um dodecaedro, o 4.° dos sólidos platônicos, é 12. Ele tem também 20 vértices e 30 arestas, sendo dual do icosaedro. Se os pontos médios das faces vizinhas de um dodecaedro regular forem unidos, por exemplo, eles formam um icosaedro regular.
 |
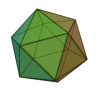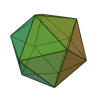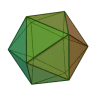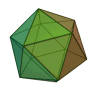O icosaedro regular pode ser visto como um antiprisma com extremos pentagonais, mais duas pirâmides pentagonais. Não é surpreendente que a presença de pentágonos regulares signifique também a presença da secção dourada. Em particular, se arestas opostas do antiprisma forem unidas, são obtidos 3 retângulos cujos lados estão no quociente dourado, com ângulos retos entre eles.
É um fato extraordinário, que à primeira vista parece absurdo, que, se um dodecaedro e um icosaedro estiverem ambos inscritos em esferas idênticas, o dodecaedro ocupe um volume maior, embora o icosaedro tenha mais faces e pareceria, por isso, naturalmente «encaixar melhor». De fato, o dodecaedro ocupa aproximadamente 66,5 % da esfera, enquanto o icosaedro ocupa apenas 60,56 %.
O dodecaedro rômbico, descrito pela primeira vez por Kepler, também tem 12 faces. Imagine cubos empacotados para preencher um espaço. Os 6 cubos adjacentes a um outro podem ser cortados em 6 pirâmides, unindo os seus centros aos vértices. Se estas pirâmides forem coladas às faces do seu cubo, cada cubo torna-se um dodecaedro rômbico e o empacotamento de dodecaedros rômbicos preenche o espaço completamente, tal como os cubos o fariam, com a diferença de que cada dodecaedro rômbico tem o dobro do volume dos cubos correspondentes.
Wells, David. Dicionário de números interessantes e curiosos. Ed. Gradiva, 1996.
30/05/2009.
Assinar:
Postagens (Atom)
