Azulejos que ensinam

Azulejos que ensinam foi o tema de uma exposição de azulejos apresentada na Universidade de Coimbra em 2007.

“Os Elementos” de Euclides foram transpostos para um conjunto de azulejos, único no mundo, que ilustram os teoremas geométricos daquele sábio grego e foram um instrumento pedagógico do ensino da Matemática pelos Jesuítas. Acredita-se que as representações reproduzidas nos azulejos em questão tenham saído da versão de André Tacquet, jesuíta e matemático belga, publicada pela primeira vez em 1654.

Pois bem, um amigo meu, Renato H. Pinto, em visita a Portugal, encontrou um catálogo com  reproduções na forma de cartão postal de seis dessas relíquias com o qual me presenteou e que, neste momento, compartilho com todos aqueles que, como eu, são apaixonados pela Geometria.

in Os Elementos de Euclides – Edição de André Tacquet, Pádua, 1729 (1ª ed: Antuérpia, 1654) Livro I, Corolário 13 da Proposição 32: Daqui se tira  um modo fácil  de dividir em três partes iguais um ângulo recto BAC. (a trissecção do ângulo reto – comentário de André Tacquet). Azulejo pertencente à coleção do Museu Nacional de Machado de Castro [Publicação autorizada pelo IMC, IP] – Fotografia; José Pessoa

in Os Elementos de Euclides – Edição de André Tacquet, Pádua, 1729 (1ª ed: Antuérpia, 1654) Livro III, Proposição 1: Dado um círculo achar-lhe o centro. Azulejo pertencente à coleção do Museu Nacional de Machado de Castro [Publicação autorizada pelo IMC, IP] – Fotografia; José Pessoa

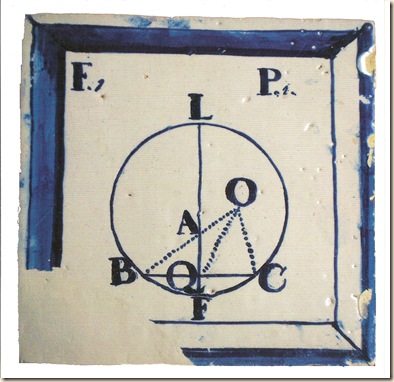
in Os Elementos de Euclides – Edição de André Tacquet, Pádua, 1729 (1ª ed: Antuérpia, 1654) Livro I, Proposição 29 (Proposição 28 nas edições actuais): Se a recta GO, cortando duas rectas AB e CF, fizer o ângulo externo GLB, igual ao interno para a mesma parte LOF, ou também os dois internos para a mesma parte BLO e LOF iguais a dois rectos, a duas rectas cortadas serão paralelas. Azulejo pertencente à coleção do Museu Nacional de Machado de Castro [Publicação autorizada pelo IMC, IP] – Fotografia; José Pessoa

in Os Elementos de Euclides – Edição de André Tacquet, Pádua, 1729 (1ª ed: Antuérpia, 1654) Livro I, Proposição 44: Sobre a recta OS construir um paralelogramo igual [em área] a um triângulo dado V, o qual [paralelogramo] tenha um ângulo igual a outro dado X. Azulejo pertencente à coleção do Museu Nacional de Machado de Castro [Publicação autorizada pelo IMC, IP] – Fotografia; José Pessoa

in Os Elementos de Euclides – Edição de André Tacquet, Pádua, 1729 (1ª ed: Antuérpia, 1654) Teoremas escolhidos de Arquimedes: Proposições 40, 41, 43, 44 (Proposições originais de André Tacquet, análogas às de Arquimedes para a esfera e o cilindro)   Proposição 4o: A superfície da esfera está para toda superfície do cone equilátero circunscrito assim como 4 está para 9. Proposição 41: A superfície total do cone equilátero circunscrito a uma esfera é quadrupla da superfície total de um outro cone semelhante inscrito na mesma esfera. Proposição 43: O cone equilátero circunscrito a uma esfera está [em volume] para o cone semelhante inscrito na mesma esfera assim como 8 está para 1. Proposição 44: A esfera está para o cone equilátero circunscrito, tanto em volume como na superfície total assim como 4 está para 9. Azulejo pertencente à coleção do Museu Nacional de Machado de Castro [Publicação autorizada pelo IMC, IP] – Fotografia; José Pessoa

in Os Elementos de Euclides – Edição de André Tacquet, Pádua, 1729 (1ª ed: Antuérpia, 1654) Teoremas escolhidos de Arquimedes: Proposição 20. Proposição 20:  As superfícies cônicas inscritas na esfera fenecem na esfera. Azulejo pertencente à coleção do Museu Nacional de Machado de Castro [Publicação autorizada pelo IMC, IP] – Fotografia; José Pessoa

 

Para mais esclarecimentos, consulte, neste blog, Os postulados de Euclides.

Também poderá ser de seu interesse consultar a versão online da edição de Oliver Byrne de “Os Elementos” de Euclides (1847)
(http://sunsite.ubc.ca/DigitalMathArchive/Euclid/byrne.html)

Francisco Ismael Reis.

14/02/2010.