Número
Um símbolo que representa uma quantidade, uma grandeza, uma posição, uma medida. Os símbolos utilizados podem ser de algarismos (26), de letras (vinte e seis) ou outros (lA), sendo que este último é uma mistura de letras e números e corresponde ao número 26 na base hexadecimal.
Número Aleatório
Número escolhido ao acaso.
Número Amigável
Número amigável é um par de números onde um deles é a soma dos divisores do outro. Como exemplo, os divisores de 220 são: 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 e 110 cuja soma é 284. Por outro lado, os divisores de 284 são: 1, 2, 4, 71 e 142 e a soma deles é 220.
Fermat descobriu também o par 17.296 e 18.416.
Descartes descobriu o par 9.363.584 e 9.437.056.
Número Ascendente
Um número natural é chamado número ascendente se cada um dos seus algarismos é estritamente maior do que qualquer um dos algarismos colocados à sua esquerda. Por exemplo, o número 3589.
Número Capicua ou Palíndromo
Um número é capicua ou palíndromo quando lido da esquerda para a direita ou da direita para a esquerda representa sempre o mesmo valor, como por exemplo 77, 434, 6446 e 82328. Para obter um número capicua a partir de outro, inverte-se a ordem dos algarismos e soma-se com o número dado, um número de vezes até que se encontre um número capicua.
Número Cardinal
É o número de elementos de um conjunto. a característica associada ao número cardinal é a cardinalidade.
Número Cíclico
Cíclicos são números que multiplicados por outro valor menor ou igual ao número de dígitos de que ele possui, seus números vão se repetindo ciclicamente, passando para o final aqueles que estão na frente.
Por exemplo: O primeiro número cíclico é o 142857.
Se este número (que possui seis dígitos) for multiplicado pelos números de 1 a 6 obtemos:
2 x 142857 = 285714 (o 1 e o 4 foram passados para o final)
3 x 142857 = 428571 (o 1 passa para o final)
4 x 142857 = 571428
5 x 142857 = 714285
6 x 142857 = 857142
Se multiplicarmos por 7 o que obtemos é 999999. Isto não é uma casualidade. Esse número (142857) é a parte periódica da divisão 1/7.
O próximo número cíclico é o 0588235294117647.
Se multiplicarmos este número pelos números de 1 a 16 acontece o mesmo que com o anterior. Se o multiplicarmos por 17 resulta em 99999999999999999.
Esses números são raros de encontrar. Outra característica curiosa destes números é a forma que se pode obtê-los:
Pegamos um número primo e calculamos seu inverso (1/p). Se a parte decimal é periódica e o período possui tantos dígitos quanto o número primo menos 1, então este é um número cíclico. Quando dividimos 1/7 se obtém 0,142857142857142857. Note que é periódico e que o período possui seis dígitos
Número Composto
É um número que tem mais do que dois divisores naturais distintos, tais como 4, 6, 12, 15, 49.
Número Decimal
Número no qual a parte inteira é separada da parte decimal por uma vírgula.
Número de Euler
Número irracional, valor da base dos logaritmos naturais. Seu valor é calculado por

Número de Mersenne
São números inteiros da forma Mp = 2p -1. Se Mp é um número primo, o numero p também é. Só são conhecidos 33 números de Mersenne. O último descoberto corresponde a p = 859 433, cujo número de Mersenne é o 2859433 - 1. Não se sabe se há um número infinito deles.
Número de Ouro
O número de ouro não é mais do que um valor numérico cujo valor aproximado é 1,618.
É obtido pela expressão:

Este número irracional é considerado por muitos o símbolo da harmonia.
Número Ímpar
Um número inteiro que não é múltiplo de 2.
Exemplos de tais números são:
..., –7, –5, –3, –1, 1, 3, 5, 7, 9, ...
Número Inteiro
Números inteiros são os números naturais e seus opostos, reunidos ao zero. ...,
–3, –2, –1, 0, 1, 2, 3, 4, 5, 6, ...
Número Irracional
Um número que não pode ser escrito sob a forma da divisão de dois números inteiros, tais como:
π = 3,14159 26535
e = 2,71828...
Número Misto
São números que misturam a escrita dos números naturais com a escrita de frações.

Número Natural
Números naturais são aqueles provenientes dos processo de contagem na natureza. Existe discussão sobre o fato do 0 (zero) ser considerado um número natural uma vez que este foi criado pelos hindús para dar sentido à nulidade de algo.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...
Número Ordinal
O ordinal de um número exprime sua posição em uma sequência, tal como primeiro, segundo, terceiro, vigésimo.
Número Par
Um número inteiro que é múltiplo de dois.
Exemplos de tais números são:
..., –6, –4, –2, 0, 2, 4, 6, 8, ...
Número Primo
Um número inteiro maior do que 1, que não é divisível por qualquer outro número exceto por ele e por 1. Um número primo tem somente dois divisores naturais diferentes.
Número Racional
Um número que pode ser colocado sobre a forma de uma fração, sendo que o numerador e o denominador devem ser dois números inteiros e o denominador não pode ser zero (0).
Número Real
Todos os números que podem ser marcados em uma reta, a reta real. Compreende os inteiros, os fracionários (conjunto dos racionais) e ainda os irracionais.
Números Regulares
Um número é dito regular se sua decomposição em fatores primos apresenta apenas potências de 2, 3 e 5.
Números Complexos
São números da forma a + bi onde a é a parte real e b o coeficiente da parte imaginária definindo-se:
i = 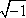
Números de Fermat
Números da forma:

Números Negativos
Todos números menores que zero.
Números Positivos
Todos os números maiores que zero.
Números Pitagóricos
São os inteiros que cumprem a equação de Pitágoras a2 + b2 = c2 . Por exemplo: 3, 4 e 5.
Números Romanos
Tipo de algarismos usado pelos romanos com a utilização de letras. Ainda hoje bastante utilizados por exemplo, para designar os séculos. Neste sistema um algarismo de menor valor colocado à esquerda subtrai ao maior: 9 é representado por 10 - 1 (IX), 90 por 100 - 10 (XC) . Se o algarismo menor está à direita do maior soma-se: 11= 10 + 1 (XI).
Números Transcendentes
São os números que não são algébricos. Não existe nenhum polinômio de coeficientes inteiros de que sejam raiz. O número Pi, por exemplo, é um número transcendente porque não se pode obtê-lo como raiz de nenhum polinômio de coeficientes inteiros. Os números transcendentes são infinitos e há muito mais do que números algébricos (que são aqueles que se podem obter como raiz de um polinômio de coeficientes inteiros). Raiz de 3 é um número algébrico, já que é solução da equação x2 - 3 = 0.
30/05/2009.


 Na situação presente, a idade do professor será representada por P e a do aluno por A;
Na situação presente, a idade do professor será representada por P e a do aluno por A; 
 Na situação presente o professor diz ao aluno:
Na situação presente o professor diz ao aluno: 




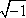



 Vemos na figura ao lado uma das curvas mais famosas e mais estranhas da Matemática. É chamada clotóide. O seu nome vem do grego Klothos (eu fio). A clotóide é a curva que se enrola e não pode parar de se enrolar.
Vemos na figura ao lado uma das curvas mais famosas e mais estranhas da Matemática. É chamada clotóide. O seu nome vem do grego Klothos (eu fio). A clotóide é a curva que se enrola e não pode parar de se enrolar.