O Triângulo de Reuleaux, também conhecido como Triângulo esférico, recebeu esse nome em homenagem a Franz Reuleaux (1829-1905), engenheiro, cientista e professor de origem alemã, o primeiro a registrar as propriedades desse triângulo.
Apesar do nome, o Triângulo de Reuleuax, não é propriamente um triângulo. Trata-se de uma forma geométrica plana, não circular, construída a partir de um triângulo equilátero.
Para a obtenção do Triângulo de Reuleaux, constróiem-se sobre os três lados de um triângulo equilátero, três arcos de circunferência com centro nos vértices do triângulo e raio de medida igual à medida do lado do triângulo.
Uma corda, ou uma corrente, suspensa por suas extremidades, presa a dois pontos fixos e sob influência exclusiva da gravidade, gera uma curva parecida com uma parábola, como conjecturou Galileu Galilei (1564-1642).
Christiaan Huygens (1629-1695), físico, matemático e astrônomo holandês, mostrou em 1646, aos 17 anos de idade, que a conjectura feita por Galileu era falsa.
A essa curva, que se parece com uma parábola,mas que não é uma parábola, foi dado o nome de catenária, termo que deriva da palavra latina catena, que significa “cadeia” ou “corrente”.
A equação matemática que descreve a catenária é dada pela seguinte função hiperbólica:
que tem como equivalente exponencial a função: 
que define uma família de curvas, entre as quais vemos algumas representadas no gráfico abaixo. 
A catenária no nosso cotidiano
A catenária está muito presente em nosso cotidiano. Ela aparece com certa frequência nas construções civis dando forma a arcos e a certas casas construidas de pedra, na construção de pontes pênsis e até mesmo no formato adquirido pela barriga de uma mulher grávida.
Veja os exemplos a seguir:
O Gateway Arch, também conhecido como Portal para o Oeste ou Portal em Arco, está situado na cidade de Saint Louis, Missouri, Estados Unidos.
O Clochán Irlandês, uma construção típica irlandesa feita de pedras.
Muitos tuneis apresentam o formato de catenária.
Assim como diversas pontes pênseis.
E redes de transmissão.
“Pitágoras nasceu em 582 a.C., em Samos. Era filho de Mnesarcos que contratou grandes homens da época, como Ferecides e Hermodamas para ensiná-lo. Pitágoras aprendeu rapidamente e, em pouco tempo, deixou para trás seus mestres matemáticos e filósofos; com dezoito anos participou dos jogos olímpicos como pugilista e ganhou todas as competições que disputou. Com mais ou menos dezenove anos, iniciou uma viagem em direção ao oriente; dirigiu-se primeiro à Babilônia onde esteve em contato com os sábios da terra, homens que pertenciam a uma raça já antiga em cultura; depois dirigiu-se à Índia onde encontrou Ciência e também a Filosofia budista, que o influenciou pelo resto de sua vida. No Egito, esteve em contato com sacerdotes do Nilo. Quando regressou à Grécia já estava com 53 anos e tornou-se líder de um movimento religioso por toda a Grécia, movimento este que tinha como base o misticismo, ritos de abstinência, pureza e meditações. Seus adeptos usavam roupas que os distinguiam das pessoas comuns. A escola pitagórica durou cerca de 150 anos, e a vida mística dos pitagóricos não impediu de fundarem a Aritmética, ou a Ciência dos Números.
Como astrônomo, foi o primeiro a afirmar que a Terra era redonda e estava suspensa no espaço, assim como os planetas giravam em torno de uma chama central à qual dava o nome de Héstia, que não era o Sol; este por sua vez recebia a luz de Héstia e a refletia. O movimento dos planetas produzia sons que nós não ouvíamos, porque estamos acostumados com eles. Com essa forma de pensar o seu sistema foi o melhor que se conheceu até Copérnico.
Obcecado por números, nos deixou a célebre frase: todas as coisas são números. Achava que o Universo era uma escala musical e ao número 1 (um) atribuía a própria essência da vida, pois tudo vem de um deus que é onipotente, onipresente e onisciente e é simplesmente um. Com sua teoria dos números, desenvolveu o estudo das notas musicais que o levou a descobrir que cordas em vibração emitem sons que dependem de seus comprimentos.
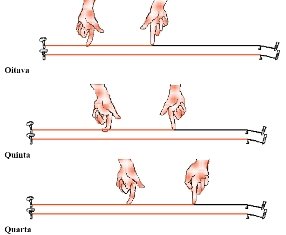Pitágoras construiu um instrumento de cordas para ensaiar e demonstrar essa teoria, acredita-se ter sido esse o primeiro instrumento de Física que existiu, em outras palavras, talvez tenha sido o primeiro experimento na história, onde a Matemática foi relacionada com a Natureza, assim como a primeira tentativa de equacionar um fenômeno natural. Ao tomar conhecimento de que as notas são obtidas por divisões da corda por números inteiros, atribuíram ao fato o significado de uma força mística. A relação entre os números e a Natureza era tão perfeita que não só os sons naturais, mas todos os eventos deveriam ser números representados por harmonias; até as órbitas dos corpos celestes estariam relacionadas aos intervalos musicais, assim os movimentos celestes representavam a Música das esferas.
Em sua sociedade secreta, os pitagóricos tinham o pentagrama, ou a estrela de cinco pontas, como emblema; não era permitida a entrada de mulheres e eles passavam os dias buscando relações matemáticas para explicar a harmonia do mundo. Também toda e qualquer descoberta feita deveria ser atribuída ao mestre e jamais revelada a uma pessoa estranha; diz-se que foi Pitágoras (ou sua sociedade) o responsável pela introdução do sistema de pesos e medidas na Grécia.
A cidade de Milos, palco principal dos pitagóricos, quando de uma revolução mais ou menos em 501 a.C., teve o governo derrubado, o palácio incendiado e vários pitagóricos foram assassinados; o próprio Pitágoras fugiu para Tarento, de onde se dirigiu para Metaponto e aí perdeu a vida numa revolta em 501 a.C. Estudos sobre Aritmética, Geometria, Música e Astronomia eram considerados fundamentais para os pitagóricos. Foi Pitágoras quem classificou a Matemática em Aritmética ou números absolutos, Música em números aplicados, Geometria em grandezas em repouso e Astronomia em grandezas em movimento,
Assim como Cristo e Sócrates, Pitágoras não escreveu qualquer trabalho que tenha chegado até nós, logo o que sabemos tem origem em três fontes:
- Os escritos de seus discípulos e seguidores como Nicomano, autor de Introdução à aritmética, onde retrata os ensinamentos dos pitagóricos.
- Nas obras de Platão que, por sua vez, foi muito influenciado pelos seguidores de Pitágoras.
- Nas obras de Aristóteles que cita e resume o pensamento pitagórico, embora muitas vezes discorde do mesmo.
A biografia de Pitágoras só foi escrita por volta de ano 300 d.C. por Diógenes Laércio, portanto muita coisa é desconhecida ou lendária.
O homem Pitágoras morreu, mas seus ensinamentos continuaram e seu trabalho foi descrito por Filolau de Tebas cerca de cem anos depois de sua morte”
Texto extraído do livro A Matemática na arte e na vida de Paulo Roberto Martins Contador – Editora Livraria da Física – 2ª edição – 2011 – Pág. 51 a 53.
Uma leitura mais que recomendada e obrigatória para todos os amantes da Matemática e para os que buscam desvendar o fascínio provocado pela Divina Proporção ou Proporção Áurea, aqui explicada com muita clareza pelo autor.
| 1º termo | 1 | |
| 2º termo | 1 | |
| 3º termo | 1+1 | 2 |
| 4º termo | 2+1 | 3 |
| 5º termo | 3+2 | 5 |
| 6º termo | 5+3 | 8 |
| 7º termo | 8+5 | 13 |
| 8º termo | 13+8 | 21 |
| 9º termo | 21+13 | 34 |
| 10º termo | 34+21 | 55 |
| 11º termo | 55+34 | 89 |
| 12º termo … | 89+55 … | 144 … |
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …A partir dos valores dessa sequência, podemos construir vários retângulos, chamados de retângulos áureos.
 Fonte: http://clubes.obmep.org.br/blog/atividade-a-razao-aurea-uma-construcao-da-espiral-aurea/ |
