O dodecaedro

O número de faces de um dodecaedro, o 4.° dos sólidos platônicos, é 12. Ele tem também 20 vértices e 30 arestas, sendo dual do icosaedro. Se os pontos médios das faces vizinhas de um dodecaedro regular forem unidos, por exemplo, eles formam um icosaedro regular.

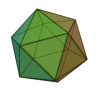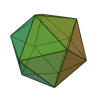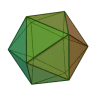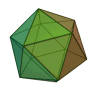O icosaedro regular pode ser visto como um antiprisma com extremos pentagonais, mais duas pirâmides pentagonais. Não é surpreendente que a pre­sença de pentágonos regulares signifique também a presença da secção dourada. Em particular, se arestas opostas do antiprisma forem unidas, são obtidos 3 retângulos cujos lados estão no quociente dourado, com ângulos retos entre eles.

É um fato extraordinário, que à primeira vista parece absurdo, que, se um dodecaedro e um icosaedro estiverem ambos inscritos em esferas idênticas, o dodecaedro ocupe um volume maior, embora o icosaedro tenha mais faces e pareceria, por isso, naturalmente «encaixar melhor». De fato, o dodecaedro ocupa aproximadamente 66,5 % da esfera, enquanto o icosaedro ocupa apenas 60,56 %.

O dodecaedro rômbico, descrito pela primeira vez por Kepler, também tem 12 faces. Imagine cubos empacotados para preencher um espaço. Os 6 cubos adjacen­tes a um outro podem ser cortados em 6 pirâmides, unindo os seus centros aos vértices. Se estas pirâmides forem coladas às faces do seu cubo, cada cubo torna-se um dodecaedro rômbico e o empacotamento de dodecaedros rômbicos preen­che o espaço completamente, tal como os cubos o fariam, com a diferença de que cada dodecaedro rômbico tem o dobro do volume dos cubos correspondentes.

Wells, David. Dicionário de números interessantes e curiosos. Ed. Gradiva, 1996.

 

30/05/2009.